Un reflector triédrico, también conocido como reflector de esquina o reflector triangular, es un dispositivo de objetivo pasivo comúnmente utilizado en antenas y sistemas de radar. Consiste en tres reflectores planos que forman una estructura triangular cerrada. Cuando una onda electromagnética incide en un reflector triédrico, se refleja en la dirección incidente, formando una onda reflejada de igual dirección, pero de fase opuesta a la onda incidente.
A continuación se presenta una introducción detallada a los reflectores de esquina triedros:
Estructura y principio:
Un reflector de esquina triedro consta de tres reflectores planos centrados en un punto de intersección común, formando un triángulo equilátero. Cada reflector plano es un espejo plano que puede reflejar las ondas incidentes según la ley de reflexión. Cuando una onda incidente incide en el reflector de esquina triedro, se refleja en cada reflector plano y finalmente forma una onda reflejada. Debido a la geometría del reflector triedro, la onda reflejada se refleja en una dirección igual pero opuesta a la de la onda incidente.
Características y aplicaciones:
1. Características de reflexión: Los reflectores de esquina triédricos presentan altas características de reflexión a una frecuencia determinada. Pueden reflejar la onda incidente con alta reflectividad, generando una señal de reflexión evidente. Debido a la simetría de su estructura, la dirección de la onda reflejada desde el reflector triédrico es igual a la dirección de la onda incidente, pero opuesta en fase.
2. Señal reflejada intensa: Dado que la fase de la onda reflejada es opuesta, cuando el reflector triedro se encuentra en dirección opuesta a la onda incidente, la señal reflejada será muy intensa. Esto convierte al reflector de esquina triedro en una aplicación importante en sistemas de radar para mejorar la señal de eco del objetivo.
3. Directividad: Las características de reflexión del reflector de esquina triedro son direccionales, es decir, solo se generará una señal de reflexión intensa en un ángulo de incidencia específico. Esto lo hace muy útil en antenas direccionales y sistemas de radar para localizar y medir la posición de objetivos.
4. Sencillo y económico: La estructura del reflector de esquina triangular es relativamente simple y fácil de fabricar e instalar. Generalmente está hecho de materiales metálicos, como aluminio o cobre, que son más económicos.
5. Campos de aplicación: Los reflectores de esquina triangulares se utilizan ampliamente en sistemas de radar, comunicaciones inalámbricas, navegación aérea, medición y posicionamiento, entre otros campos. Pueden utilizarse como antenas de identificación de objetivos, de medición de distancias, de radiogoniometría y de calibración, entre otros.
A continuación presentaremos este producto en detalle:
Para aumentar la directividad de una antena, una solución bastante intuitiva es usar un reflector. Por ejemplo, si empezamos con una antena de alambre (digamos, una antena dipolo de media onda), podríamos colocar una lámina conductora detrás para dirigir la radiación hacia adelante. Para aumentar aún más la directividad, se puede usar un reflector de esquina, como se muestra en la Figura 1. El ángulo entre las placas será de 90 grados.
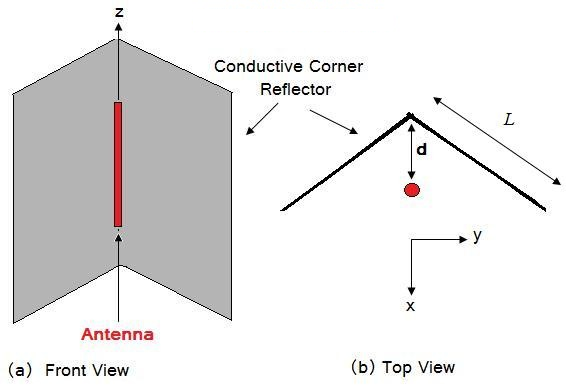
Figura 1. Geometría del reflector de esquina.
El diagrama de radiación de esta antena puede comprenderse mediante la teoría de imágenes y, posteriormente, calculando el resultado mediante la teoría de matrices. Para facilitar el análisis, asumiremos que las placas reflectantes tienen una extensión infinita. La Figura 2 a continuación muestra la distribución de la fuente equivalente, válida para la región situada delante de las placas.
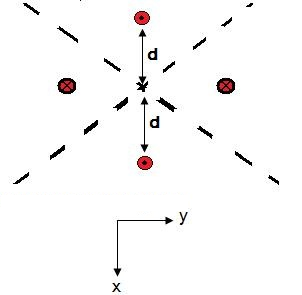
Figura 2. Fuentes equivalentes en el espacio libre.
Los círculos punteados indican antenas que están en fase con la antena real; las antenas marcadas con una x están 180 grados fuera de fase con respecto a la antena real.
Supongamos que la antena original tiene un patrón omnidireccional dado por ( ). Entonces, el patrón de radiación (R) del "conjunto equivalente de radiadores" de la Figura 2 se puede escribir como:
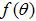
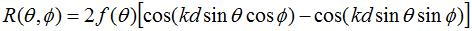
Lo anterior se desprende directamente de la Figura 2 y la teoría de matrices (k es el número de onda). El patrón resultante tendrá la misma polarización que la antena polarizada verticalmente original. La directividad aumentará entre 9 y 12 dB. La ecuación anterior proporciona los campos radiados en la región frente a las placas. Dado que asumimos que las placas eran infinitas, los campos detrás de las placas son cero.
La directividad será máxima cuando d sea la mitad de la longitud de onda. Suponiendo que el elemento radiante de la Figura 1 es un dipolo corto con un patrón dado por ( ), los campos para este caso se muestran en la Figura 3.
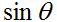
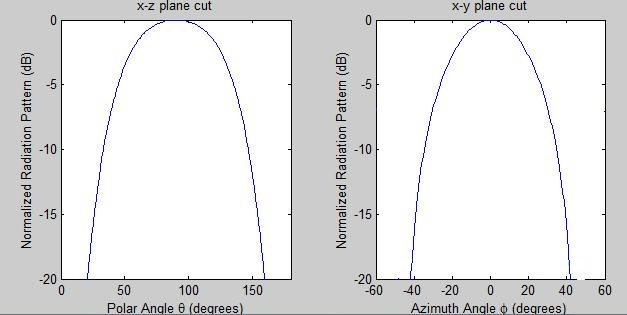
Figura 3. Patrones polares y azimutales del patrón de radiación normalizado.
El patrón de radiación, la impedancia y la ganancia de la antena se verán influenciados por la distancia.dde la Figura 1. La impedancia de entrada aumenta con el reflector cuando la separación es de media longitud de onda; se puede reducir acercando la antena al reflector. La longitudLLos reflectores de la Figura 1 suelen ser 2*d. Sin embargo, si se traza un rayo que viaja a lo largo del eje y desde la antena, este se reflejará si la longitud es al menos ( ). La altura de las placas debe ser mayor que la del elemento radiante; sin embargo, dado que las antenas lineales no radian bien a lo largo del eje z, este parámetro no es crucial.
Reflector de esquina triédricoIntroducción del producto en serie:
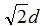
Hora de publicación: 12 de enero de 2024













